2023年高考数学（理科）西藏试卷及答案

2023年高考数学（理科）西藏试卷及答案解析

小编整理了2023年高考数学（理科）西藏试卷及答案，数学是人类对事物的抽象结构与模式进行严格描述的一种通用手段，可以应用于现实世界的任何问题。下面是小编为大家整理的2023年高考数学（理科）西藏试卷及答案，希望能帮助到大家!

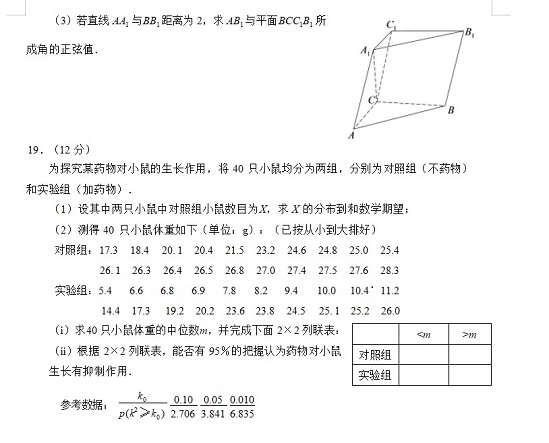
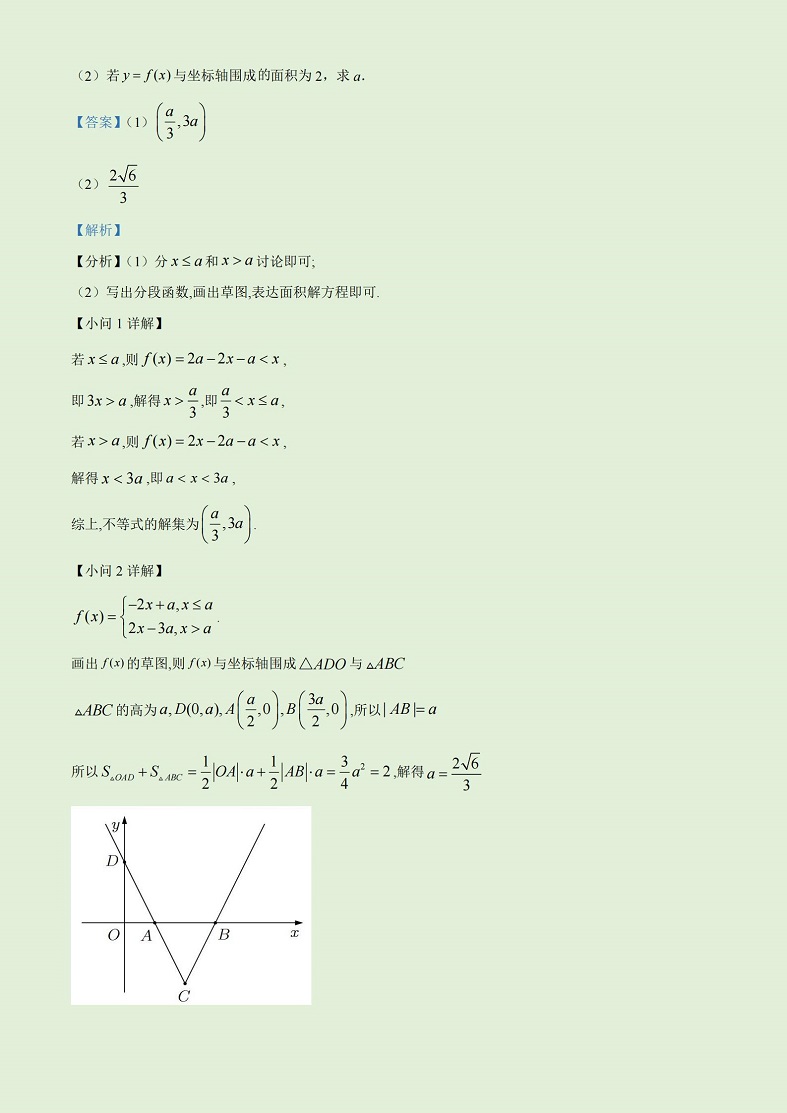
2023年高考数学（理科）西藏试卷及答案

高中数学中有关等差、等比数列的知识点

1、等差数列{an}的任意连续m项的和构成的数列Sm、S2m—Sm、S3m—S2m、S4m—S3m、……仍为等差数列。

2、等差数列{an}中，若m+n=p+q，则

3、等比数列{an}中，若m+n=p+q，则

4、等比数列{an}的任意连续m项的和构成的数列Sm、S2m—Sm、S3m—S2m、S4m—S3m、……仍为等比数列。

5、两个等差数列{an}与{bn}的和差的数列{an+bn}、{an—bn}仍为等差数列。

6、两个等比数列{an}与{bn}的积、商、倒数组成的数列仍为等比数列。

7、等差数列{an}的任意等距离的项构成的数列仍为等差数列。

8、等比数列{an}的任意等距离的项构成的数列仍为等比数列。

9、三个数成等差数列的设法：a—d，a，a+d;四个数成等差的设法：a—3d，a—d，，a+d，a+3d

10、三个数成等比数列的设法：a/q，a，aq;

四个数成等比的错误设法：a/q3，a/q，aq，aq3(为什么?)

高中数学知识点

一、平面的基本性质与推论

1、平面的基本性质：

公理1如果一条直线的两点在一个平面内，那么这条直线在这个平面内;

公理2过不在一条直线上的三点，有且只有一个平面;

公理3如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

2、空间点、直线、平面之间的位置关系：

直线与直线—平行、相交、异面;

直线与平面—平行、相交、直线属于该平面(线在面内，最易忽视);

平面与平面—平行、相交。

3、异面直线：

平面外一点A与平面一点B的连线和平面内不经过点B的直线是异面直线(判定);

所成的角范围(0，90)度(平移法，作平行线相交得到夹角或其补角);

两条直线不是异面直线，则两条直线平行或相交(反证);

异面直线不同在任何一个平面内。

求异面直线所成的角：平移法，把异面问题转化为相交直线的夹角

二、空间中的平行关系

1、直线与平面平行(核心)

定义：直线和平面没有公共点

判定：不在一个平面内的一条直线和平面内的一条直线平行，则该直线平行于此平面(由线线平行得出)

性质：一条直线和一个平面平行，经过这条直线的平面和这个平面相交，则这条直线就和两平面的交线平行

2、平面与平面平行

定义：两个平面没有公共点

判定：一个平面内有两条相交直线平行于另一个平面，则这两个平面平行

性质：两个平面平行，则其中一个平面内的直线平行于另一个平面;如果两个平行平面同时与第三个平面相交，那么它们的交线平行。

3、常利用三角形中位线、平行四边形对边、已知直线作一平面找其交线

三、空间中的垂直关系

1、直线与平面垂直

定义：直线与平面内任意一条直线都垂直

判定：如果一条直线与一个平面内的两条相交的直线都垂直，则该直线与此平面垂直

性质：垂直于同一直线的两平面平行

推论：如果在两条平行直线中，有一条垂直于一个平面，那么另一条也垂直于这个平面

直线和平面所成的角：【0，90】度，平面内的一条斜线和它在平面内的射影说成的锐角，特别规定垂直90度，在平面内或者平行0度

2、平面与平面垂直

定义：两个平面所成的二面角(从一条直线出发的两个半平面所组成的图形)是直二面角(二面角的平面角：以二面角的棱上任一点为端点，在两个半平面内分别作垂直于棱的两条射线所成的角)

判定：一个平面过另一个平面的垂线，则这两个平面垂直

性质：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直