五年级上册数学第四单元测试卷及答案

人教版五年级上册数学第四单元测试卷及答案

在五年级这个学习阶段,一次次的检测题,是一次次的进步,也是一次次成绩提高的关键。以下是小编准备的一些五年级上册数学第四单元测试卷及答案，仅供参考。

五年级上册数学第四单元测试卷

1.有红、蓝、绿各1个球放入箱中,任意摸出一个球,可能出现(　　)种结果。

2.盒子中有8个球,分别是5个红球、1个绿球和2个黄球,任意摸出一个,可能摸到的是(　　)球,也可能摸到(　　)球或(　　)球,摸到(　　)球的可能性最大,摸到(　　)球的可能性最小。

3.一个正方体,四个面上写着“1”,一个面上写着“2”,一个面上写着“3”。抛一次,写着(　　)的面朝上的可能性最大,写着(　　)的面和写着(　　)的面朝上的可能性一样大。

4.往盒子里放两种颜色的球,共8个,任意摸1个,要使摸到绿球和蓝球的可能性相等,绿球应放(　　)个,蓝球应放(　　)个。

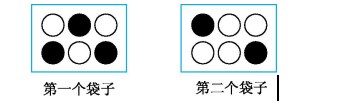
5.在下面袋子里任意摸一个球,第一个袋子里摸到白球和黑球的可能性(　　),在第二个袋子里摸到白球和黑球的可能性(　　)。

6.在括号里填“可能”“不可能”或“一定”。

(1)玻璃杯从很高的地方落在水泥地面上,玻璃杯(　　)会破碎。

(2)明天(　　)会下雨。

(3)公鸡(　　)下蛋。

二、选择题。(把正确答案的序号填在括号里)

1.2008年奥运会(　　)在北京举行。

A.一定　　 B.不可能　　 C.可能

2.小明妈妈的年龄(　　)比小明大。

A.不可能 B.可能 C.一定

3.妈妈的身高(　　)比女儿高。

A.一定 B.不一定 C.不可能

4.三位数加三位数,和(　　)是四位数。

A.可能 B.一定 C.不可能

5.给一个正方体的表面涂上红、黄、蓝三种颜色,任意抛一次,使红色面朝上的可能性最大,蓝色面和黄色面朝上的可能性相等,需要有(　　)个面涂红色。

A.2　　　　 B.3　　　 　C.4

6.某超市为了促销商品,组织了一次摸奖活动,设置一等奖5名,二等奖15名,三等奖200名。消费者摸到(　　)等奖的可能性最大。

A.一 B.二 C.三

三、解决问题。

1.一个口袋里有5个球,分别是1个红球,3个蓝球和1个绿球,闭上眼睛,从口袋里摸出1个球,摸到哪种颜色球的可能性最大?

2.在一个袋子中装有同一种形状的20粒纽扣,其中黑的有6粒,蓝的有4粒,红的有10粒。(如下图)

(1)摸出1粒时,可能出现哪几种结果?列举出来。

(2)摸出1粒时,摸到哪种颜色纽扣的可能性最大?

(3)摸出11粒时,其中一定有什么颜色的?

3.一个盒子里有形状、大小完全一样的5块奶糖,8块水果糖和3块巧克力糖,任意摸1块糖,摸到什么糖的可能性最小?

4.在口袋里放进红、蓝两种铅笔共10支。任意摸一支,摸到红铅笔算甲赢,摸到蓝铅笔算乙赢。你认为口袋里应该放多少支红铅笔,游戏才是公平?

5.桌上放有7张牌,标号分别为1(A),2,3,4,5,6,7,现在把牌面朝下放在桌上。每次任意拿出一张,拿到单数算甲赢,拿到双数算乙赢。这个游戏规则公平吗?如果不公平,请你修改规则,使游戏公平。

6.请你动手设计一个转盘,使指针停在红色区域的可能性最大,停在黄色区域的可能性最小。

五年级上册数学第四单元测试卷参考答案

一、 1. 3　2.红　绿　黄　红　绿　3. 1　2　3 4. 4　4　5.相等　不相等

6. (1)一定　(2)可能　(3)不可能

二、 1. A　2. C　3. B　4. A　5. C　6. C

三、 1.蓝球

2. (1)黑、蓝、红　(2)红　(3)红

3. 巧克力糖

4. 各放5支

5.不公平,这里的单数有1,3,5,7四种,双数有2,4,6三种,所以不公平。可以将规则修改为大于4的算甲赢,小于4的算乙赢。(答案不唯一)

6.略

小学五年级数学解题技巧

1、对照法

如何正确地理解和运用数学概念?小学数学常用的方法就是对照法。根据数学题意，对照概念、性质、定律、法则、公式、名词、术语的含义和实质，依靠对数学知识的理解、记忆、辨识、再现、迁移来解题的方法叫做对照法。

这个方法的思维意义就在于，训练学生对数学知识的正确理解、牢固记忆、准确辨识。

例1：三个连续自然数的和是18，则这三个自然数从小到大分别是多少?

对照自然数的概念和连续自然数的性质可以知道：三个连续自然数和的平均数就是这三个连续自然数的中间那个数。

例2：判断题：能被2除尽的数一定是偶数。

这里要对照“除尽”和“偶数”这两个数学概念。只有这两个概念全理解了，才能做出正确判断。

2、公式法

运用定律、公式、规则、法则来解决问题的方法。它体现的是由一般到特殊的演绎思维。公式法简便、有效，也是小学生学习数学必须学会和掌握的一种方法。但一定要让学生对公式、定律、规则、法则有一个正确而深刻的理解，并能准确运用。

例3：计算59×37+12×59+59

59×37+12×59+59

=59×(37+12+1)…………运用乘法分配律

=59×50…………运用加法计算法则

=(60-1)×50…………运用数的组成规则

=60×50-1×50…………运用乘法分配律

=3000-50…………运用乘法计算法则

=2950…………运用减法计算法则

3、比较法

通过对比数学条件及问题的异同点，研究产生异同点的原因，从而发现解决问题的方法，叫比较法。

比较法要注意：

(1)找相同点必找相异点，找相异点必找相同点，不可或缺，也就是说，比较要完整。

(2)找联系与区别，这是比较的实质。

(3)必须在同一种关系下(同一种标准)进行比较，这是“比较”的基本条件。

(4)要抓住主要内容进行比较，尽量少用“穷举法”进行比较，那样会使重点不突出。

(5)因为数学的严密性，决定了比较必须要精细，往往一个字，一个符号就决定了比较结论的对或错。

例4：填空：0.75的位是()，这个数小数部分的位是();十分位的数4与十位上的数4相比，它们的()相同，()不同，前者比后者小了()。

这道题的意图就是要对“一个数的位和小数部分的位的区别”，还有“数位和数值”的区别等。

例5：六年级同学种一批树，如果每人种5棵，则剩下75棵树没有种;如果每人种7棵，则缺少15棵树苗。六年级有多少学生?

这是两种方案的比较。相同点是：六年级人数不变;相异点是：两种方案中的条件不一样。

找联系：每人种树棵数变化了，种树的总棵数也发生了变化。

找解决思路(方法)：每人多种7-5=2(棵)，那么，全班就多种了75+15=90(棵)，全班人数为90÷2=45(人)。

4、分类法

根据事物的共同点和差异点将事物区分为不同种类的方法，叫做分类法。分类是以比较为基础的。依据事物之间的共同点将它们合为较大的类，又依据差异点将较大的类再分为较小的类。

分类即要注意大类与小类之间的不同层次，又要做到大类之中的各小类不重复、不遗漏、不交叉。

例6：自然数按约数的个数来分，可分成几类?

答：可分为三类。(1)只有一个约数的数，它是一个单位数，只有一个数1;(2)有两个约数的，也叫质数，有无数个;(3)有三个约数的，也叫合数，也有无数个。

5、分析法

把整体分解为部分，把复杂的事物分解为各个部分或要素，并对这些部分或要素进行研究、推导的一种思维方法叫做分析法。

依据：总体都是由部分构成的。

思路：为了更好地研究和解决总体，先把整体的各部分或要素割裂开来，再分别对照要求，从而理顺解决问题的思路。

也就是从求解的问题出发，正确选择所需要的两个条件，依次推导，一直到问题得到解决为止，这种解题模式是“由果溯因”。分析法也叫逆推法。常用“枝形图”进行图解思路。

例7：玩具厂计划每天生产200件玩具，已经生产了6天，共生产1260件。问平均每天超过计划多少件?

思路：要求平均每天超过计划多少件，必须知道：计划每天生产多少件和实际每天生产多少件。计划每天生产多少件已知，实际每天生产多少件，题中没有告诉，还得求出来。要求实际每天生产多少件玩具，必须知道：实际生产多少天，和实际生产多少件，这两个条件题中都已知。