高考甲卷物理试题与答案解析2023

全国高考甲卷物理试题与答案解析2023

今年高考物理设计与体育运动相联系的试题情境，引导学生增强体育健康意识，促进学生德智体美劳全面发展。下面是小编为大家整理的关于高考甲卷物理试题与答案解析，欢迎大家来阅读。

2023高考甲卷物理真题及答案解析

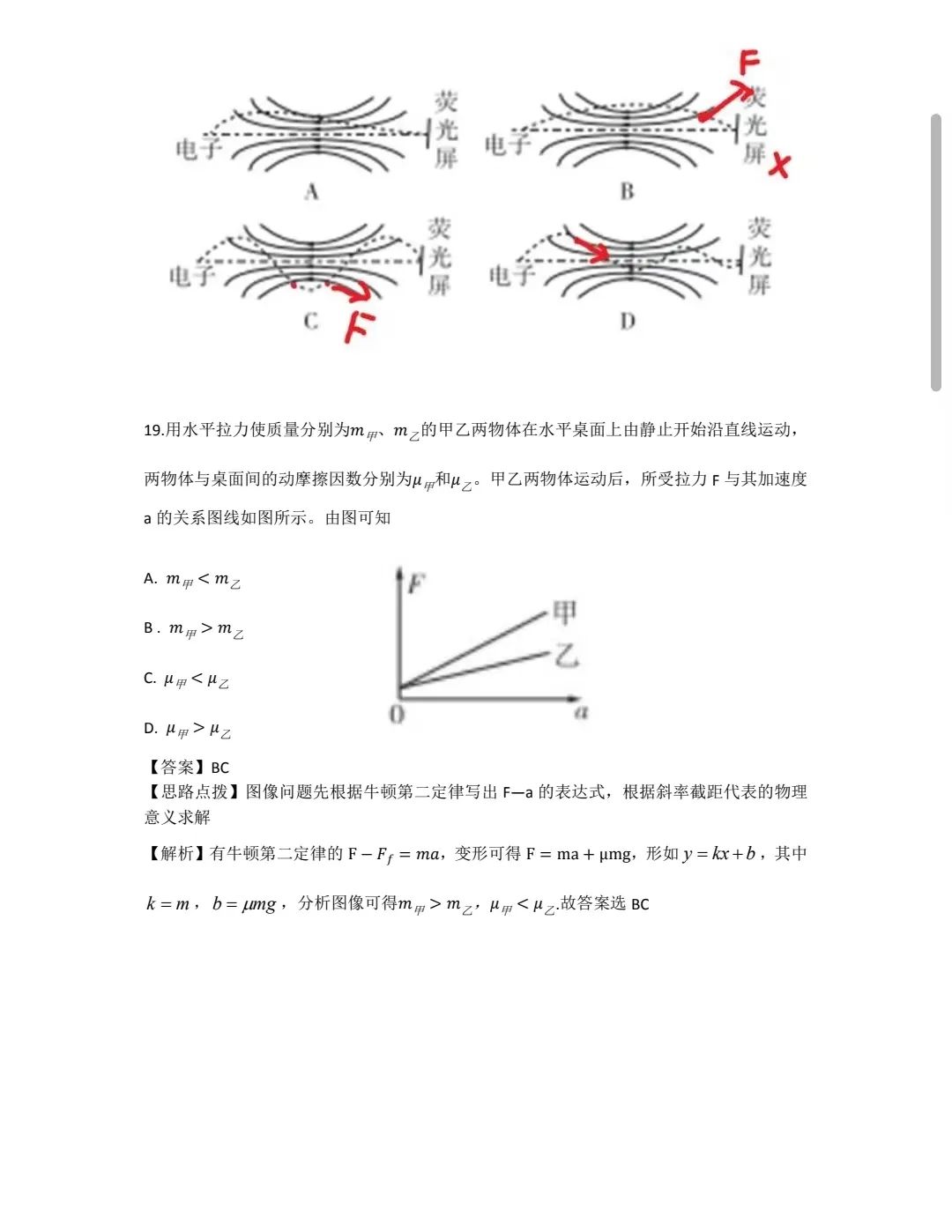
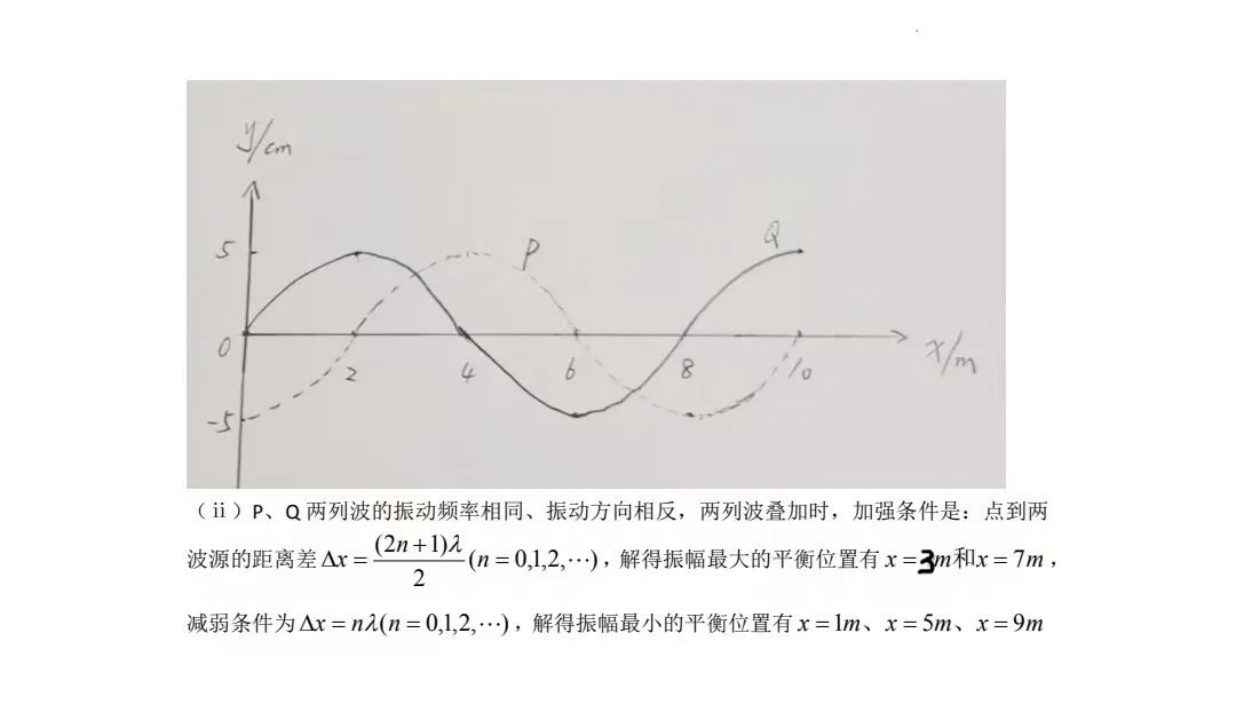
高考物理必考公式

一、力的合成与分解公式

1.同一直线上力的合成同向:F=F1+F2， 反向：F=F1-F2 (F1>F2)

2.互成角度力的合成：

F=(F12+F22+2F1F2cosα)1/2(余弦定理) F1⊥F2时:F=(F12+F22)1/2

3.合力大小范围：|F1-F2|≤F≤|F1+F2|

4.力的正交分解：Fx=Fcosβ，Fy=Fsinβ(β为合力与x轴之间的夹角tgβ=Fy/Fx)

二、运动和力公式

1.牛顿第一运动定律(惯性定律)：物体具有惯性，总保持匀速直线运动状态或静止状态,直到有外力迫使它改变这种状态为止

2.牛顿第二运动定律：F合=ma或a=F合/ma{由合外力决定,与合外力方向一致}

3.牛顿第三运动定律：F=-F′{负号表示方向相反,F、F′各自作用在对方，平衡力与作用力反作用力区别，实际应用：反冲运动}

4.共点力的平衡F合=0，推广 {正交分解法、三力汇交原理｝

5.超重：FN>G，失重：FN

6.牛顿运动定律的适用条件：适用于解决低速运动问题，适用于宏观物体，不适用于处理高速问题，不适用于微观粒子

三、匀速圆周运动公式

1.线速度V=s/t=2πr/T

2.角速度ω=Φ/t=2π/T=2πf

3.向心加速度a=V2/r=ω2r=(2π/T)2r

4.向心力F心=mV2/r=mω2r=mr(2π/T)2=mωv=F合

5.周期与频率：T=1/f

6.角速度与线速度的关系：V=ωr

7.角速度与转速的关系ω=2πn(此处频率与转速意义相同)

8.主要物理量及单位：弧长(s):米(m);角度(Φ)：弧度(rad);频率(f)：赫(Hz);周期(T)：秒(s);转速(n)：r/s;半径(r):米(m);线速度(V)：m/s;角速度(ω)：rad/s;向心加速度：m/s2。

四、平抛运动公式

1.水平方向速度：Vx=Vo

2.竖直方向速度：Vy=gt

3.水平方向位移：x=Vot

4.竖直方向位移：y=gt2/2

5.运动时间t=(2y/g)1/2(通常又表示为(2h/g)1/2)

6.合速度Vt=(Vx2+Vy2)1/2=[Vo2+(gt)2]1/2，合速度方向与水平夹角β:tgβ=Vy/Vx=gt/V0

7.合位移：s=(x2+y2)1/2,位移方向与水平夹角α:tgα=y/x=gt/2Vo

8.水平方向加速度：ax=0;竖直方向加速度：ay=g

五、竖直上抛运动公式

1.位移s=Vot-gt2/2

2.末速度Vt=Vo-gt (g=9.8m/s2≈10m/s2)

3.有用推论Vt2-Vo2=-2gs

4.上升最大高度Hm=Vo2/2g(抛出点算起)

5.往返时间t=2Vo/g (从抛出落回原位置的时间)

六、自由落体运动公式

1.初速度Vo=0

2.末速度Vt=gt

3.下落高度h=gt2/2(从Vo位置向下计算) 4.推论Vt2=2gh

匀变速直线运动公式

1.平均速度V平=s/t(定义式)

2.有用推论Vt2-Vo2=2as

3.中间时刻速度Vt/2=V平=(Vt+Vo)/2

4.末速度Vt=Vo+at

5.中间位置速度Vs/2=[(Vo2+Vt2)/2]1/2

6.位移s=V平t=Vot+at2/2=Vt/2t

7.加速度a=(Vt-Vo)/t {以Vo为正方向，a与Vo同向(加速)a>0;反向则a<0｝

8.实验用推论Δs=aT2 {Δs为连续相邻相等时间(T)内位移之差｝

9.主要物理量及单位:初速度(Vo):m/s;加速度(a):m/s2;末速度(Vt):m/s;时间(t)秒(s);位移(s):米(m);路程:米;速度单位换算：1m/s=3.6km/h。

高考物理知识点总结

1、机械运动：一个物体相对于另一个物体的位置的改变叫做机械运动，简称运动，它包括平动，转动和振动等运动形式。为了研究物体的运动需要选定参照物(即假定为不动的物体)，对同一个物体的运动，所选择的参照物不同，对它的运动的描述就会不同，通常以地球为参照物来研究物体的运动。

2、质点：用来代替物体的只有质量没有形状和大小的点，它是一个理想化的物理模型。仅凭物体的大小不能做视为质点的依据。

3、位移和路程：位移描述物体位置的变化，是从物体运动的初位置指向末位置的有向线段，是矢量。路程是物体运动轨迹的长度，是标量。

路程和位移是完全不同的概念，仅就大小而言，一般情况下位移的大小小于路程，只有在单方向的直线运动中，位移的大小才等于路程。

4、速度和速率

(1)速度：描述物体运动快慢的物理量是矢量。

①平均速度：质点在某段时间内的位移与发生这段位移所用时间的比值叫做这段时间(或位移)的平均速度v，即v=s/t，平均速度是对变速运动的粗略描述。

②瞬时速度：运动物体在某一时刻(或某一位置)的速度，方向沿轨迹上质点所在点的切线方向指向前进的一侧。瞬时速度是对变速运动的精确描述。

(2)速率：①速率只有大小，没有方向，是标量。

②平均速率：质点在某段时间内通过的路程和所用时间的比值叫做这段时间内的平均速率。在一般变速运动中平均速度的大小不一定等于平均速率，只有在单方向的直线运动，二者才相等。

5、加速度

(1)加速度是描述速度变化快慢的物理量，它是矢量。加速度又叫速度变化率。

(2)定义：在匀变速直线运动中，速度的变化Δv跟发生这个变化所用时间Δt的比值，叫做匀变速直线运动的加速度，用a表示。

(3)方向：与速度变化Δv的方向一致。但不一定与v的方向一致。[注意]加速度与速度无关。只要速度在变化，无论速度大小，都有加速度;只要速度不变化(匀速)，无论速度多大，加速度总是零;只要速度变化快，无论速度是大、是小或是零，物体加速度就大。

6、匀速直线运动(1)定义：在任意相等的时间内位移相等的直线运动叫做匀速直线运动。

(2)特点：a=0，v=恒量。(3)位移公式：S=vt。

7、匀变速直线运动(1)定义：在任意相等的时间内速度的变化相等的直线运动叫匀变速直线运动。

(2)特点：a=恒量(3)公式：速度公式：V=V0+at位移公式：s=v0t+at2

速度位移公式：vt2-v02=2as平均速度V=

以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值。

8、重要结论

(1)匀变速直线运动的质点，在任意两个连续相等的时间T内的位移差值是恒量，即

ΔS=Sn+l–Sn=aT2=恒量

(2)匀变速直线运动的质点，在某段时间内的中间时刻的瞬时速度，等于这段时间内的平均速度，即：

9、自由落体运动

(1)条件：初速度为零，只受重力作用。(2)性质：是一种初速为零的匀加速直线运动，a=g。

(3)公式：

10、运动图像

(1)位移图像(s-t图像)：①图像上一点切线的斜率表示该时刻所对应速度;

②图像是直线表示物体做匀速直线运动，图像是曲线则表示物体做变速运动;

③图像与横轴交叉，表示物体从参考点的一边运动到另一边。

(2)速度图像(v-t图像)：①在速度图像中，可以读出物体在任何时刻的速度;

②在速度图像中，物体在一段时间内的位移大小等于物体的速度图像与这段时间轴所围面积的值。

③在速度图像中，物体在任意时刻的加速度就是速度图像上所对应的点的切线的斜率。

④图线与横轴交叉，表示物体运动的速度反向。

⑤图线是直线表示物体做匀变速直线运动或匀速直线运动;图线是曲线表示物体做变加速运动。

高考物理学习方法

1、重点扫除知识“盲点”

对照考纲，把新课学习时不太清楚的知识点全部都弄清楚，把已经弄清楚的进一步熟练。其中包括物理概念，定理、定律，所有的公式，搞清楚它们的来龙去脉，能够进行推导。避免涉及到基本知识时不能把握题目的真正意图，或选择题不能够正确的辨析，计算题用错公式，张冠李戴等。

2、基本题型反复熟练

每一种基本题型，每一种基本模型，都要重新过手，要做到“三不”，即：不怕麻烦、不怕重复、不厌其烦。比如：追击问题、传送带问题，板块模型、动生电模型、感生电模型等逐一梳理，绝不遗漏。

3、厘清力学三条主线

● 牛顿定律——整个力学的基石。它确立了运动与力之间最本质的关系，受什么力就会做什么运动。搞清楚了这个问题，就搞清楚了力学的根本。

● 能量观点——主要涉及动能定理、能量守恒定律(包含机械能守恒定律)。能量观点解决问题比牛顿定律更“高端”，它能够解决一些牛顿定律在高中阶段不能解决的问题(如变速率曲线运动)或者更加方便的解决一些牛顿定律不便于解决的问题(如复杂的多过程问题)。

● 动量观点——包括动量定理，动量守恒定律。注意区分动量定理与动能定理，以及各自擅长解决的问题;注意区分能量守恒定律与动量守恒定律，以及它们各自擅长解决的问题。

厘清了这三条力学的线索，同时也就解决了电学一半的问题。

4、课本和考纲是“秘籍”

复习过程中，不能脱离教材，教材要认真阅读，而且要精读。包括教材上的那些装置、情境图，还有课后的练习题。选修3-3(热学)、选修3-4(振动、波、光学)、选修3-5近代物理部分(波粒二象性、原子原子核)，这几部分的教材更要反复地阅读、梳理、并熟练记忆。

5、需要攻克“实验堡垒”

实验既是重点，更是难点。复习中，所有的实验，都要从实验目的入手，知道实验设计的来龙去脉，知道为什么这样设计，还可以有什么变化。切忌死记硬背。只有这样才能在考试中，以“变”应“变”。

6、定时训练是“磨刀石”

复习之后即时的定时训练，既可以有效地检查复习的效果，以便即时进行弥补，又可以训练解题的速度，提高熟练程度，这一点必须长期坚持。